1994 MCM A:The Communications Network Problem
In your company, information is shared among departments on a daily basis. This information includes the previous day’s sales statistics and current production guidance. It is important to get this information out as quickly as possible.
Suppose that a communications network is to be used to transfer blocks of data (files) from one computer to another. As an example, consider the graph model in Figure 1.

Vertices $V_1, V_2,...,V_m$ represent computers, and edges $e_1, e_2,...,e_n$ represent files to be transferred (between computers represented by edge endpoints). $T(e_x)$ is the time that it takes to transfer file $e_x$, and $C(V_y)$ is the capacity of the computer represented by $V_y$ to transfer files simultaneously. A file transfer involves the engagement of both computers for the entire time that it takes to transfer the file. For example, $C(V_y)=1$ means that computer $V_y$ can be involved in only one transfer at a time.
We are interested in scheduling the transfers in an optimal way, to minimize the total time that it takes to complete them all. This minimum total time is called the makespan. Consider the three following situations for your company:
Situation A
Your corporation has 28 departments. Each department has a computer, each of which is represented by a vertex in Figure 2. Each day, 27 files must be transferred, represented by the edges in Figure 2. For this network, $T(e_x)=1$ and $C(V_y)=1$ for all $x$ and $y$. Find an optimal schedule and the makespan for the given network. Can you prove to your supervisor that your makespan is the smallest possible (optimal) for the given network? Describe your approach to solving the problem. Does your approach work for the general case, that is, where $T(e_x)$, $C(V_y)$, and the graph structure are arbitrary?

Situation B
Suppose that your company changes the requirements for data transfer. You must now consider the same basic network structure (again, see Figure 2) with different types and sizes of files. These files take the amount of time to transfer indicated in Table 2 by the $T(e_x)$ terms for each edge. We still have $C(V_y)=1$ for all $y$. Find an optimal schedule and the makespan for the new network. Can you prove that your makespan is the smallest possible for the new network? Describe your approach to solving this problem. Does your approach work for the general case? Comment on any peculiar or unexpected results.

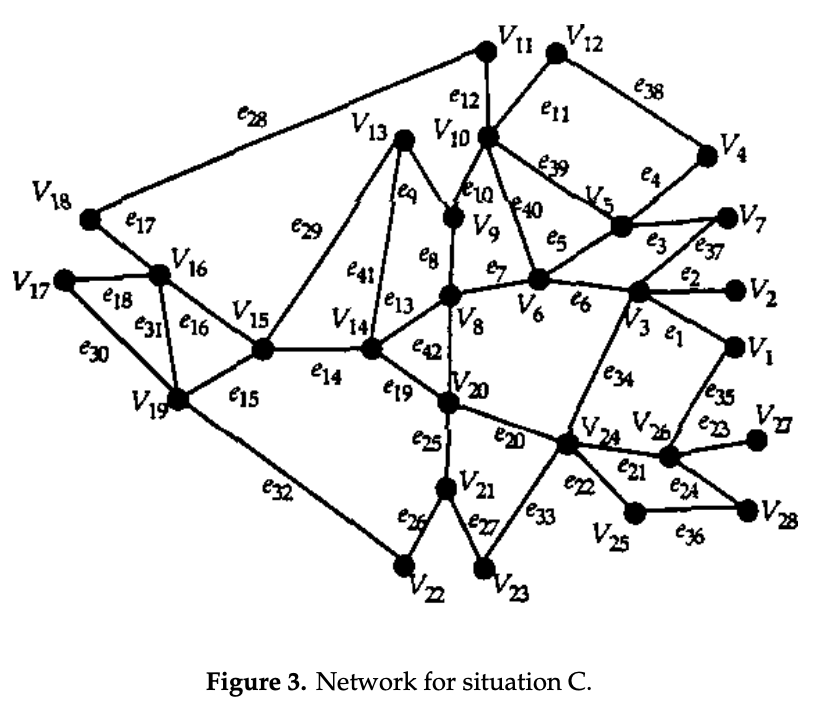
Situation C
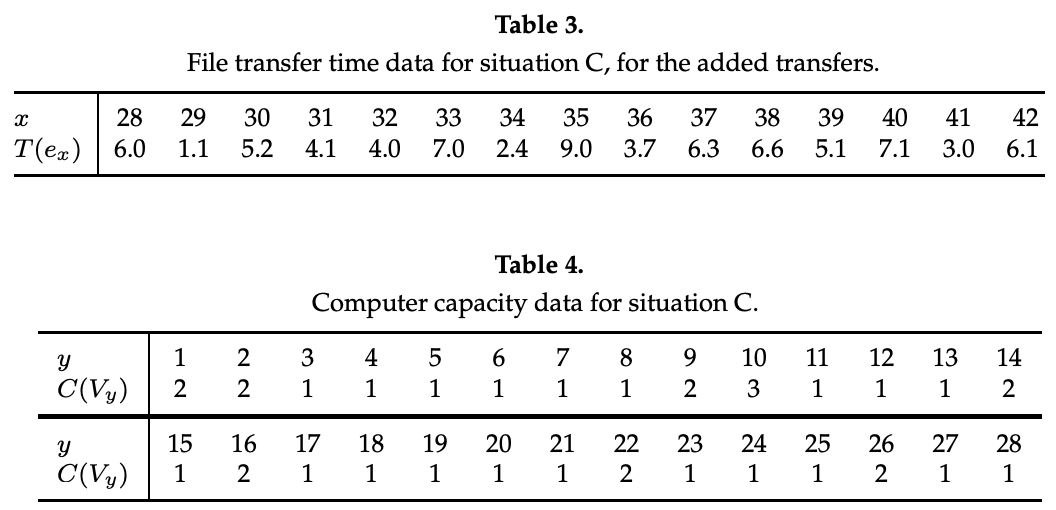
Your corporation is considering expansion. If that happens, there are several new files (edges) that will need to be transferred daily. This expansion will also include an upgrade of the computer system. Some of the 28 departments will get new computers that can handle more than one transfer at a time. All of these changes are indicated in Figure 3 and Tables 3–4. What is the best schedule and makespan that you can find? Can you prove that your makespan is the smallest possible for this network? Describe your approach to solving the problem. Comment on any peculiar or unexpected results.