抢渡长江
(全国竞赛2003年D题)
“渡江”是武汉城市的一张名片。1934年9月9日,武汉警备旅官兵与体育界人士联手,在武汉第一次举办横渡长江游泳竞赛活动,起点为武昌汉阳门码头,终点设在汉口三北码头,全程约5000米。有44人参加横渡,40人达到终点,张学良将军特意向冠军获得者赠送了一块银盾,上书“力挽狂澜”。
2001年,“武汉抢渡长江挑战赛”重现江城。2002年,正式命名为“武汉国际抢渡长江挑战赛”,于每年的5月1日进行。由于水情、水性的不可预测性,这种竞赛更富有挑战性和观赏性。
2002年5月1日,抢渡的起点设在武昌汉阳门码头,终点设在汉阳南岸咀,江面宽约1160米。据报载,当日的平均水温16.8℃, 江水的平均流速为1.89米/秒。参赛的国内外选手共186人(其中专业人员将近一半),仅34人到达终点,第一名的成绩为14分8秒。除了气象条件外,大部分选手由于路线选择错误,被滚滚的江水冲到下游,而未能准确到达终点。
假设在竞渡区域两岸为平行直线, 它们之间的垂直距离为1160米, 从武昌汉阳门的正对岸到汉阳南岸咀的距离为1000米,见示意图。
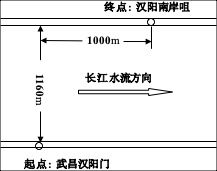
请你们通过数学建模来分析上述情况, 并回答以下问题:
- 假定在竞渡过程中游泳者的速度大小和方向不变,且竞渡区域每点的流速均为1.89 米/秒。试说明2002年第一名是沿着怎样的路线前进的,求她游泳速度的大小和方向。如何根据游泳者自己的速度选择游泳方向,试为一个速度能保持在1.5米/秒的人选择游泳方向,并估计他的成绩。
- 在(1)的假设下,如果游泳者始终以和岸边垂直的方向游, 他(她)们能否到达终点?根据你们的数学模型说明为什么1934年和2002年能游到终点的人数的百分比有如此大的差别;给出能够成功到达终点的选手的条件。
- 若流速沿离岸边距离的分布为(设从武昌汉阳门垂直向上为 $y$ 轴正向) :
$$ v(y)=\left\{\begin{array}{ll} 1.47米/秒, & 0米\le y\le 200米,\\ 2.11米/秒, & 200米< y< 960米,\\ 1.47米/秒, & 960米\le y\le 1160米.\\ \end{array}\right. $$ 游泳者的速度大小(1.5米/秒)仍全程保持不变,试为他选择游泳方向和路线,估计他的成绩。 - 若流速沿离岸边距离为连续分布, 例如
$$ v(y)=\left\{\begin{array}{ll} \frac{2.28}{200}y, & 0\le y\le 200,\\ 2.28, & 200< y < 960,\\ \frac{2.28}{200}(1160-y), & 960\le y\le 1160.\\ \end{array}\right. $$ 或你们认为合适的连续分布,如何处理这个问题。 - 用普通人能懂的语言,给有意参加竞渡的游泳爱好者写一份竞渡策略的短文。
- 你们的模型还可能有什么其他的应用?