非线性交调设计
(全国竞赛1993年A题)
如果一非线性器件的输入 $u(t)$ 与输出 $y(t)$ 的关系是 $y(t)=u(t)+u^2(t)$,其中 $t$ 是时间,那么当输入是包含频率 $f_1,f_2$ 的信号 $u(t)=\cos 2\pi f_1 t+\cos 2\pi f_2 t$ 时,输出 $y(t)$ 中不仅包含输入信号 $f_1,f_2$, 而且还会出现 $2f_1,f_1\pm f_2$ 等新的频率成分,这些新的频率称为交调。如果交调出现在原有频率 $f_1,f_2$ 的附近,就会形成噪声干扰,因此工程设计中对交调的出现有一定的要求。
现有一SCS(非线性)系统,其输入和输出由下一组数据给出:
| 输入$u(t)$ | 0 | 5 | 10 | 20 | 30 | 40 | 50 | 60 | 80 |
| 输出$y(t)$ | 0 | 2.25 | 6.80 | 20.15 | 35.70 | 56.40 | 75.10 | 87.85 | 98.50 |
输入信号为 $u(t)=A_1\cos 2\pi f_1t+A_2\cos 2\pi f_2t+A_3\cos 2\pi f_3t$,其中 $A_1=25, A_2=10, A_3=45$ 是输入信号的振幅,对输入信号的频率 $f_1,f_2,f_3$ 的设计要求为:
- $36\le f_1\le 40$, $41\le f_2\le 50$, $46\le f_3\le 53$
- 输出中的交调均不得出现在 $f_i\pm5$ 的范围内,$i=1,2,3$,此范围称为 $f_i$ 的接收带,参见下图。
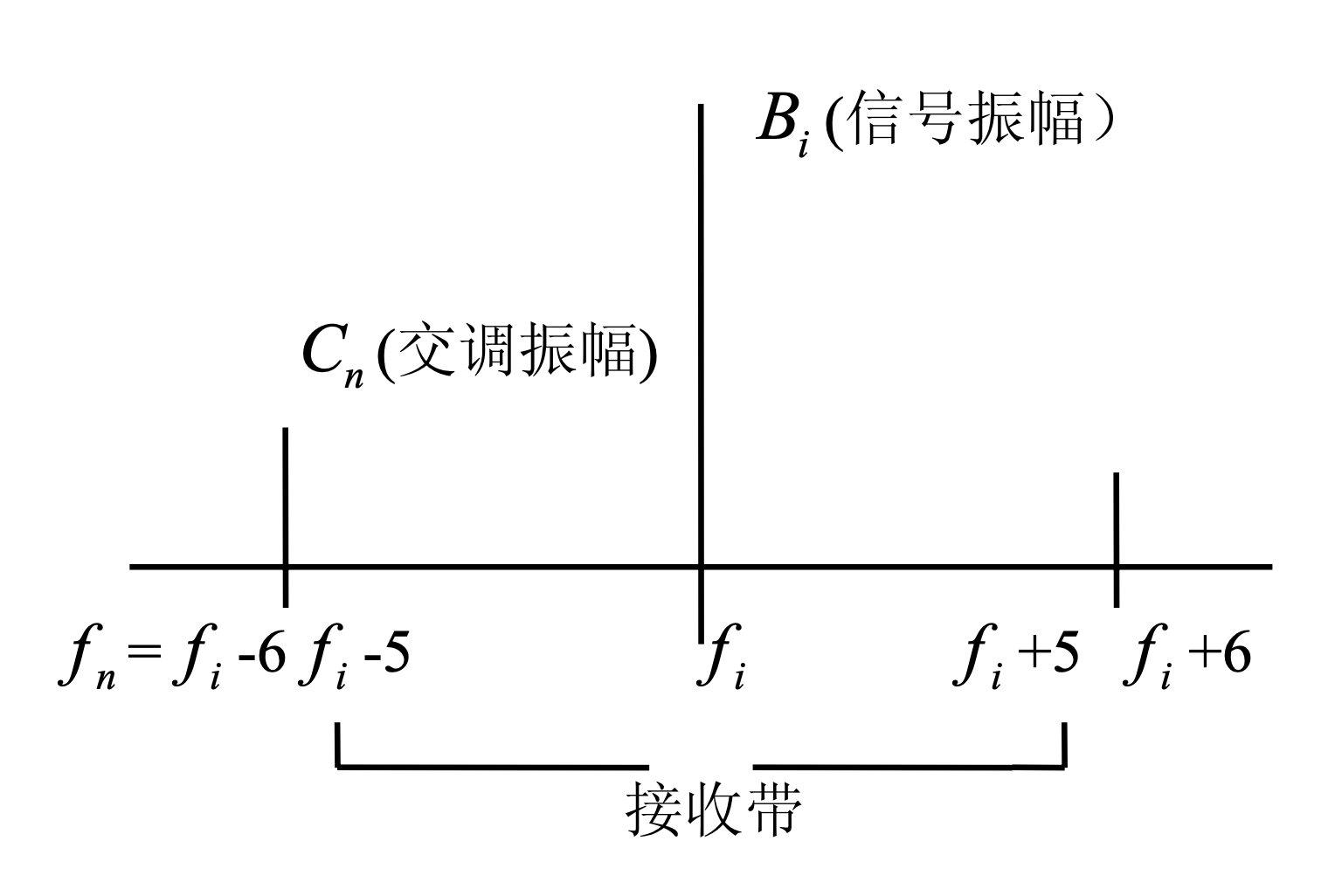
- 定义输出中的信噪比 $SNR=10\log_{10}\frac{B_i^2}{C_n^2}$(单位:分贝), 其中 $B_i$ 是输出中对应于频率 $f_i$ 的信号的振幅,$C_n$ 是某一频率为 $f_n$ 的交调的振幅。若 $f_n$ 出现在 $f_n=f_i\pm6$ 处则对应的 $SNR$ 应大于10分贝。(参见上图)
- $f_i$ 不得出现在 $f_j$ 的接收带内,$i,j=1,2,3$, $i\ne j$.
- 为简单起见,$f_i$ 只取整数值,且交调只考虑二阶类型,(即 $f_i\pm f_j$,$i,j=1,2,3$)和三阶类型(即$f_i\pm f_j\pm f_k$, $i,j,k=1,2,3$)。
试按上述要求设计输入信号频率$f_1,f_2,f_3$.
