空洞探测
(全国竞赛2000年D题)
山体、隧洞、坝体等的某些内部结构可用弹性波测量来确定。一个简化问题可描述为,一块均匀介质构成的矩形平板内有一些充满空气的空洞,在平板的两个邻边分别等距地设置若干波源,在它们的对边对等地安放同样多的接收器,记录弹性波由每个波源到达对边上每个接收器的时间,根据弹性波在介质中和在空气中不同的传播速度,来确定板内空洞的位置。现考察如下的具体问题:
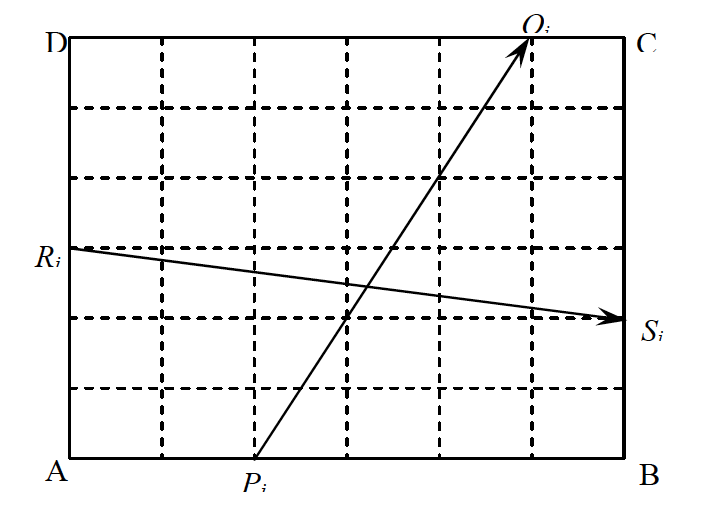
一块 $240(米)\times 240(米)$ 的平板(如图),在 $AB$ 边等距地设置7个波源$P_i(i=1,\cdots,7)$,$CD$ 边对等地安放7个接收器 $Q_j(j=1,\cdots,7)$,记录由 $P_i$ 发出的弹性波到达 $Q_j$ 的时间 $t_{ij}$ (秒); 在 $AD$ 边等距地设置7个波源 $R_i(i=1,\cdots,7)$,$BC$ 边对等地安放7个接收器$S_j(j=1,\cdots,7)$,记录由 $R_i$ 发出的弹性波到达 $S_j$ 的时间 $\tau_{ij}$ (秒)。已知弹性波在介质和空气中的传播速度分别为2880(米/秒)和320(米/秒),且弹性波沿板边缘的传播速度与在介质中的传播速度相同。
- 确定该平板内空洞的位置。
- 只根据由 $P_i$ 发出的弹性波到达 $Q_j$ 的时间 $t_{ij}(i,j=1,\cdots,7)$,能确定空洞的位置吗;讨论在同样能够确定空洞位置的前提下,减少波源和接受器的方法。
| $t_{ij}$ | $Q_1$ | $Q_2$ | $Q_3$ | $Q_4$ | $Q_5$ | $Q_6$ | $Q_7$ |
| $P_1$ | 0.0611 | 0.0895 | 0.1996 | 0.2032 | 0.4181 | 0.4923 | 0.5646 |
| $P_2$ | 0.0989 | 0.0592 | 0.4413 | 0.4318 | 0.4770 | 0.5242 | 0.3805 |
| $P_3$ | 0.3052 | 0.4131 | 0.0598 | 0.4153 | 0.4156 | 0.3563 | 0.1919 |
| $P_4$ | 0.3221 | 0.4453 | 0.4040 | 0.0738 | 0.1789 | 0.0740 | 0.2122 |
| $P_5$ | 0.3490 | 0.4529 | 0.2263 | 0.1917 | 0.0839 | 0.1768 | 0.1810 |
| $P_6$ | 0.3807 | 0.3177 | 0.2364 | 0.3064 | 0.2217 | 0.0939 | 0.1031 |
| $P_7$ | 0.4311 | 0.3397 | 0.3566 | 0.1954 | 0.0760 | 0.0688 | 0.1042 |
| $\tau_{ij}$ | $S_1$ | $S_2$ | $S_3$ | $S_4$ | $S_5$ | $S_6$ | $S_7$ |
| $R_1$ | 0.0645 | 0.0602 | 0.0813 | 0.3516 | 0.3867 | 0.4314 | 0.5721 |
| $R_2$ | 0.0753 | 0.0700 | 0.2852 | 0.4341 | 0.3491 | 0.4800 | 0.4980 |
| $R_3$ | 0.3456 | 0.3205 | 0.0974 | 0.4093 | 0.4240 | 0.4540 | 0.3112 |
| $R_4$ | 0.3655 | 0.3289 | 0.4247 | 0.1007 | 0.3249 | 0.2134 | 0.1017 |
| $R_5$ | 0.3165 | 0.2409 | 0.3214 | 0.3256 | 0.0904 | 0.1874 | 0.2130 |
| $R_6$ | 0.2749 | 0.3891 | 0.5895 | 0.3016 | 0.2058 | 0.0841 | 0.0706 |
| $R_7$ | 0.4434 | 0.4919 | 0.3904 | 0.0786 | 0.0709 | 0.0914 | 0.0583 |
